삽입 정렬(Insertion Sort)이란?
두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료와 비교해 삽입할 위치를 결정하는 알고리즘
즉, 두 번째 자료는 첫 번째 자료와, 세 번째 자료는 두 번째와 첫 번째 자료와 비교를 해 삽입될 위치를 찾는다. 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한 칸씩 뒤로 이동시킨다.
처음 Key값은 두 번째 자료부터 시작한다.
예시
배열에 3, 7, 2, 5, 1, 4가 있다고 가정하고 자료를 오름차순으로 정렬해보자.
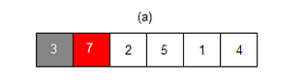
1. key: 7(두 번째 자료). 첫 번째 값인 3과 비교한다.

2. key: 2(세 번째 자료). 두 번째 값인 7과 비교해 7을 한 칸 뒤로 이동한다. 첫 번째 값인 3과 비교하고 3을 한 칸 뒤로 이동한다. 2를 첫 번째 자리에 넣는다.

3. key: 5(네 번째 자료). 세 번째 값인 7과 비교한 후, 7을 한 칸 뒤로 이동한다. 두 번째 값인 3과 비교한 후, 5를 세 번째 자리에 넣는다.

4. key: 1(다섯 번째 자료). 네 번째 값인 7과 비교한 후, 7을 한 칸 뒤로 이동한다. 세 번째 값인 5와 비교한 후, 5를 한 칸 뒤로 이동한다. 두 번째 값인 3과 비교한 후, 3을 한 칸 뒤로 이동한다. 첫 번째 값인 2와 비교한 후, 2를 한 칸 뒤로 이동하고 1을 첫 번째 자리에 넣는다.

5. key: 4(여섯 번째 자료). 다섯 번째 값인 7과 비교한 후, 7을 한 칸 뒤로 이동한다. 네 번째 값인 5와 비교한 후, 5를 한 칸 뒤로 이동한다. 세 번째 값인 3과 비교한 후, 4를 네 번째 자리에 넣는다.

장점
- 안정 정렬(Stable Sort)
- 데이터의 수가 적을 경우 알고리즘 자체가 간단하므로 다른 복잡한 정렬 방법보다 유리함
- 대부분의 원소가 이미 정렬되어 있는 경우 매우 효율적
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않음 -> 제자리 정렬(in-place sorting)
단점
- 비교적 많은 레코드들의 이동을 포함
- 레코드의 수가 많고 레코드 크기가 클 경우 적합하지 않음
시간복잡도
- 최선의 경우
- 비교 횟수
- 1번 씩의 비교만 이루어진다. -> (n-1)번
- T(n) = O(n)
- 비교 횟수
- 최악의 경우
- 비교 횟수
- 각 반복마다 i번의 비교 수행
- 1 + 2 + ... + (n-1) = n(n-1)/2 = O(n^2)
- 교환 횟수
- 각 반복마다 (i+2)번의 이동 발생
- n(n-1) + 2(n-1) = (n^2+3n-4)/2 = O(n^2)
- T(n) = O(n^2)
- 비교 횟수
정렬 알고리즘 시간복잡도 비교

간단하지만 비효율적인 방법
삽입 정렬, 선택 정렬, 버블 정렬
복잡하지만 효율적인 방법
퀵 정렬, 힙 정렬, 합병 정렬
삽입정렬 JS 코드
function solution(arr) {
let answer = arr;
for (let i = 1; i < arr.length; i++) {
let key = arr[i];
let j;
for (j = i - 1; j >= 0; j--) {
if (key <= arr[j]) {
arr[j + 1] = arr[j];
} else {
break;
}
}
arr[j + 1] = key;
}
return answer;
}
'Algorithm > Data Structure, Algorithm' 카테고리의 다른 글
| [알고리즘][파이썬] 소수 판별 알고리즘(에라토스테네스의 체) (0) | 2022.04.14 |
|---|---|
| [자료구조][JS] 선택 정렬(Selection Sort) (0) | 2021.08.29 |
| [자료구조][JS] 스택, 큐 - push(), pop(), shift() (0) | 2021.08.22 |
| [알고리즘][JS] 해쉬 알고리즘 - JS ES6 Map() (0) | 2021.08.08 |
| 투포인터 알고리즘, 슬라이딩 윈도우 (0) | 2021.07.25 |